Convergence of the integration error with MC and QMC.

在本文结束时，我的目标是让你相信：如果你需要使用随机数，你应该考虑使用scipy.stats.qmc而不是np.random.

在以下内容中，我们假设SciPy、NumPy和Matplotlib已安装并导入

import numpy as np
from scipy.stats import qmc
import matplotlib.pyplot as plt

请注意，这些示例中没有使用种子。这将是另一篇文章的主题：播种只应用于测试目的。

那么什么是蒙特卡罗（MC）和准蒙特卡罗（QMC）呢？

蒙特卡罗（MC）#

MC 方法是一类广泛的计算算法，它们依赖于重复的随机抽样来获得数值结果。其基本概念是利用随机性来解决原则上可能是确定性的问题。它们常用于物理和数学问题，在难以或不可能使用其他方法时最为有用。MC 方法主要用于三类问题：优化、数值积分和从概率分布中生成抽样。

简而言之，这就是通常使用 MC 生成样本点的方式

rng = np.random.default_rng()
sample = rng.random(size=(256, 2))

在这种情况下，sample是一个包含 256 个点的二维数组，可以使用二维散点图对其进行可视化。

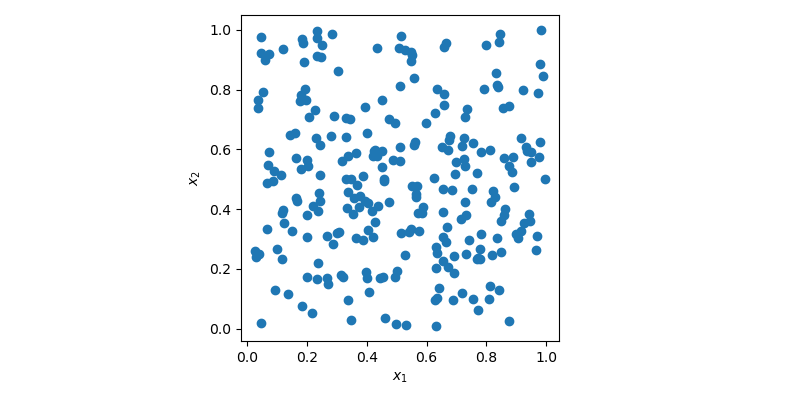
MC sample using a 2D scatter plot.

在上图中，点是随机生成的，没有任何关于先前绘制点的知识。很明显，空间的某些区域未被探索，而其他区域则有集群。在优化问题中，这可能意味着你需要生成更多样本才能找到最佳值。或者在回归问题中，你可能会因为某些点的集群而过度拟合模型。

生成随机数比听起来更复杂。简单的 MC 方法旨在对点进行抽样，使其独立且同分布 (IID)。

有人可能会认为，解决方案就是使用网格！但是看看如果我们在单位超立方体 (所有边界范围从 0 到 1) 中的点之间有 0.1 的距离会发生什么。

disc = 10
x1 = np.linspace(0, 1, disc)
x2 = np.linspace(0, 1, disc)
x3 = np.linspace(0, 1, disc)
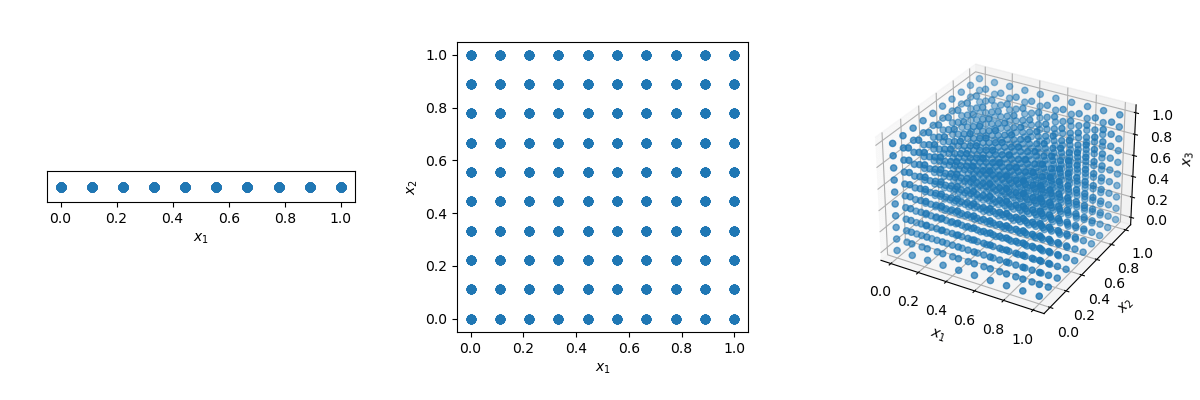
x1, x2, x3 = np.meshgrid(x1, x2, x3)

填充单位区间的点数将是 10 个。在二维超立方体中，相同的间距将需要 100 个点，在三维空间中需要 1,000 个点。随着维数的增加，填充空间所需的样本数量呈指数增长，因为空间的维数随着增加而增加。这种指数增长称为维数灾难。

Curse of dimensionality. 3 figures: 1D, 2D and 3D scatter plots of samples.

准蒙特卡罗（QMC）#

为了缓解维数灾难，你可以决定从样本中随机删除点或在 n 维空间中随机抽样。在这两种情况下，这将需要清空某些区域并在其他地方聚集点。

准蒙特卡罗 (QMC) 方法专门为解决这个问题而创建。与 MC 方法相反，QMC 方法是确定性的。这意味着点不是 IID，而是每个新点都知道先前点。结果是我们可以构建具有良好空间覆盖率的样本。

确定性不意味着样本总是相同的。序列可以被扰乱。

从 1.7 版本开始，SciPy 在 scipy.stats.qmc 中提供了 QMC 方法。

让我们使用 MC 和名为Sobol’ 的 QMC 方法生成 2 个样本。

n, d = 256, 2

rng = np.random.default_rng()
sample_mc = rng.random(size=(n, d))

qrng = qmc.Sobol(d=d)
sample_qmc = qrng.random(n=n)

一个非常相似的接口，但正如下面所见，结果截然不同。

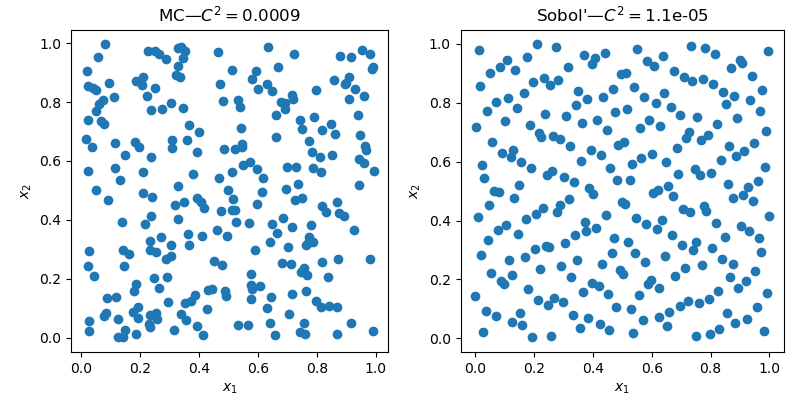
Comparison between MC and QMC samples using a 2D scatter plot.

二维空间明显表现出更少的空区域和更少的 QMC 样本集群。

质量？#

除了质量的视觉改进之外，还有指标可以评估样本的质量。通常使用几何标准，可以计算所有点对之间的距离 (L1、L2 等)。但也有一些统计标准，例如：差异.

qmc.discrepancy(sample_mc)
# 0.0009
qmc.discrepancy(sample_qmc)
# 1.1e-05

值越低，质量越好。

收敛#

如果这仍然不能说服你，让我们来看一个具体的例子：积分函数。让我们看看 5 维空间中平方和的平均值

$$f(\mathbf{x}) = \left( \sum_{j=1}^{5}x_j \right)^2,$$

其中 $x_j \sim \mathcal{U}(0,1)$。它有一个已知的平均值，$\mu = 5/3+5(5-1)/4$。通过对点进行抽样，我们可以数值计算该平均值。

抽样进行 99 次并取平均值。为了简单起见，没有报告方差，只需知道它在 QMC 中保证比在 MC 中低。

dim = 5
ref = 5 / 3 + 5 * (5 - 1) / 4
n_conv = 99
ns_gen = 2 ** np.arange(4, 13)


def func(sample):
    # dim 5, true value 5/3 + 5*(5 - 1)/4
    return np.sum(sample, axis=1) ** 2


def conv_method(sampler, func, n_samples, n_conv, ref):
    samples = [sampler(n_samples) for _ in range(n_conv)]
    samples = np.array(samples)

    evals = [np.sum(func(sample)) / n_samples for sample in samples]
    squared_errors = (ref - np.array(evals)) ** 2
    rmse = (np.sum(squared_errors) / n_conv) ** 0.5

    return rmse


# Analysis
sample_mc_rmse = []
sample_sobol_rmse = []
rng = np.random.default_rng()

for ns in ns_gen:
    # Monte Carlo
    sampler_mc = lambda x: rng.random((x, dim))
    conv_res = conv_method(sampler_mc, func, ns, n_conv, ref)
    sample_mc_rmse.append(conv_res)

    # Sobol'
    engine = qmc.Sobol(d=dim)
    conv_res = conv_method(engine.random, func, ns, 1, ref)
    sample_sobol_rmse.append(conv_res)

sample_mc_rmse = np.array(sample_mc_rmse)
sample_sobol_rmse = np.array(sample_sobol_rmse)

# Plot
fig, ax = plt.subplots(figsize=(4, 4))
ax.set_aspect("equal")

# MC
ratio = sample_mc_rmse[0] / ns_gen[0] ** (-1 / 2)
ax.plot(ns_gen, ns_gen ** (-1 / 2) * ratio, ls="-", c="k")

ax.scatter(ns_gen, sample_mc_rmse, label="MC: np.random")

# Sobol'
ratio = sample_sobol_rmse[0] / ns_gen[0] ** (-2 / 2)
ax.plot(ns_gen, ns_gen ** (-2 / 2) * ratio, ls="-", c="k")

ax.scatter(ns_gen, sample_sobol_rmse, label="QMC: qmc.Sobol")

ax.set_xlabel(r"$N_s$")
ax.set_xscale("log")
ax.set_xticks(ns_gen)
ax.set_xticklabels([rf"$2^{{{ns}}}$" for ns in np.arange(4, 13)])

ax.set_ylabel(r"$\log (\epsilon)$")
ax.set_yscale("log")

ax.legend(loc="upper right")
fig.tight_layout()
plt.show()

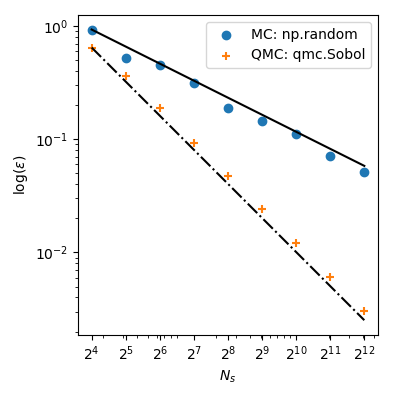
Convergence of the integration error with MC and QMC.

对于 MC，近似误差遵循 $O(n^{-1/2})$ 的理论速率。但是，QMC 方法具有更好的收敛速率，并为该函数实现了 $O(n^{-1})$——对于非常平滑的函数，甚至具有更好的速率。

这意味着使用来自Sobol’ 的 $2^8=256$ 个点会导致比使用来自 MC 的 $2^{12}=4096$ 个点产生更低的误差！当函数评估成本很高时，这可以带来巨大的计算节省。

从任何分布中抽样 (高级)#

但还有更多！QMC 的另一个用途是抽取任意分布。在 SciPy 1.8 中，有新的 采样器 类，允许你从任何自定义分布中抽样。其中一些方法可以使用 qrvs 方法使用 QMC

以下是一个使用 SciPy 中的分布（fisk）的示例。我们从该分布中生成一个 MC 样本（直接从分布中使用 fisk.rvs 或使用 NumericalInverseHermite.rvs）以及另一个使用 QMC 使用 NumericalInverseHermite.qrvs 生成的样本。

import scipy.stats as stats
from scipy.stats import sampling

# Any distribution
c = 3.9
dist = stats.fisk(c)

# MC
rng = np.random.default_rng()
sample_mc = dist.rvs(128, random_state=rng)

# QMC
rng_dist = sampling.NumericalInverseHermite(dist)
# sample_mc = rng_dist.rvs(128, random_state=rng)  # MC alternative same as above
qrng = qmc.Sobol(d=1)
sample_qmc = rng_dist.qrvs(128, qmc_engine=qrng)

让我们通过计算经验概率密度函数 (PDF) 来可视化 MC 和 QMC 之间的差异。QMC 结果明显优于 MC。

# Visualization
fig, axs = plt.subplots(1, 2, sharey=True, sharex=True, figsize=(8, 4))

x = np.linspace(dist.ppf(0.01), dist.ppf(0.99), 100)
pdf = dist.pdf(x)
delta = np.max(pdf) * 5e-2

samples = {"MC: np.random": sample_mc, "QMC: qmc.Sobol": sample_qmc}

for ax, sample in zip(axs, samples):
    ax.set_title(sample)
    ax.plot(x, pdf, "-", lw=3, label="fisk PDF")
    ax.plot(samples[sample], -delta - delta * np.random.random(128), "+k")

    kde = stats.gaussian_kde(samples[sample])
    ax.plot(x, kde(x), "-.", lw=3, label="empirical PDF")
    # or use a histogram
    # ax.hist(sample, density=True, histtype='stepfilled', alpha=0.2)
    ax.set_xlim([0, 3])

axs[0].legend(loc="best")
fig.supylabel("Density")
fig.supxlabel("Sample value")
fig.tight_layout()
plt.show()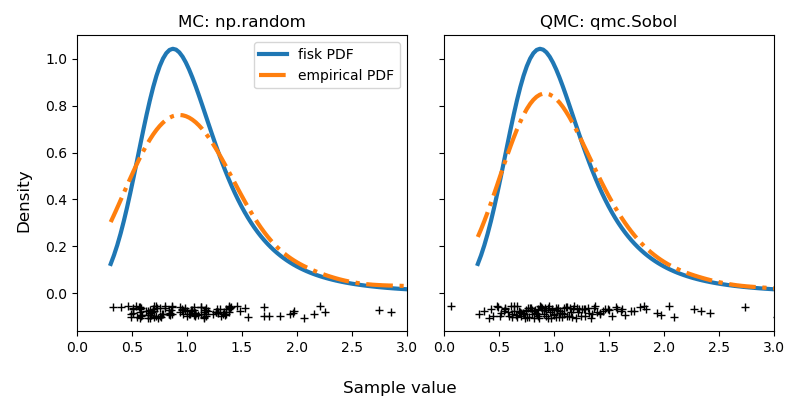

Probability density function of the fisk distribution.\nComparison with empirical distributions built with MC and QMC.

细心的读者会注意到没有播种。这是有意为之，正如本文开头提到的。你可能会再次运行此代码，并在 MC 中获得更好的结果。但只有在某些情况下。这正是我要说明的。平均而言，你保证使用 QMC 获得更一致的结果和更好的质量。我建议你尝试一下，亲眼看看！

结论#

我希望说服你在下次需要随机数时使用 QMC。QMC 优于 MC，句号。

存在大量文献和严格的证明。MC 仍然更流行的原因之一是 QMC 难以实现，并且根据方法的不同，需要遵循一些规则。

以我们使用的Sobol’ 方法为例：你必须使用正好 $2^n$ 个样本。如果你没有这样做，你将破坏一些属性，最终获得与 MC 相同的性能。这就是为什么有些人争论说 QMC 并不更好：他们只是没有正确使用这些方法，因此没有看到任何好处并得出结论，认为 MC “足够”。

在 scipy.stats.qmc 中，我们竭尽全力解释如何使用这些方法，并且添加了一些明确的警告，以使这些方法对每个人都易于访问和使用。