这篇文章包含了自上一篇关于VF2++的文章以来的所有主要更新。每个部分都致力于一个不同的子问题，并展示了迄今为止的进展。总体进展、里程碑和相关问题可以在此处找到。

节点排序#

节点排序是VF2++提出的一个主要修改。基本上，节点按照一个顺序进行检查，该顺序通过首先检查更可能匹配的节点来加快匹配速度。算法的这部分已经实现，但是存在一个问题。分离节点（未连接到图的其余部分）的存在会导致代码崩溃。修复此错误将是后续步骤中的重中之重。排序实现由以下伪代码描述。

匹配顺序

  1. 设置 $M = \varnothing$。
  2. 设置 $\bar{V1}$：尚未排序的节点
  3. 当 $\bar{V1}$ 不为空 时
    • $rareNodes=[$来自 $V_1$ 的标签最稀有的节点$]$
    • $maxNode=argmax_{degree}(rareNodes)$
    • $T=$ 以 $maxNode$ 为根的广度优先搜索树
    • 对于 $T$ 中的每一层 时
      • $V_d=[$第 $d$ 层的节点$]$
      • $\bar{V_1} \setminus V_d$
      • $ProcessLevel(V_d)$
  4. 输出 $M$：节点的匹配顺序。

处理层级

  1. 当 $V_d$ 不为空 时
    • $S=[$来自 $V_d$ 的在 M 中拥有最多邻居的节点$]$
    • $maxNodes=argmax_{degree}(S)$
    • $rarestNode=[$来自 $maxNodes$ 的标签最稀有的节点$]$
    • $V_d \setminus m$
    • 将 m 附加到 M

$T_i$ 和 $\tilde{T_i}$#

根据 VF2++ 论文中的符号

$$T_1=(u\in V_1 \setminus m: \exists \tilde{u} \in m: (u,\tilde{u}\in E_1))$$

其中 $V_1$ 和 $E_1$ 分别包含第一个图的所有节点和边，而 $m$ 是一个字典，将第一个图的每个节点映射到第二个图的节点。现在，如果我们解释上述等式，我们得出结论，$T_1$ 包含已覆盖节点的未覆盖邻居。简单来说，它包含所有尚未属于映射 $m$ 的节点，但它们是属于映射中的节点的邻居。此外，

$$\tilde{T_1}=(V_1 \setminus m \setminus T_1)$$

下图旨在提供对 $T_i$ 究竟是什么的一些视觉解释。

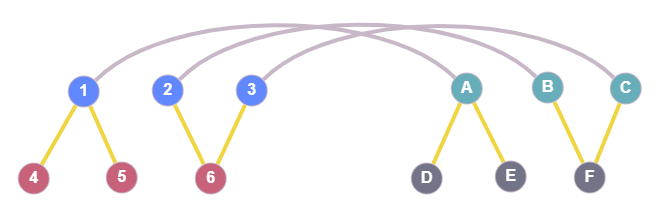
Illustration of $T_i$.

蓝色节点 1、2、3 是来自图 G1 的节点，绿色节点 A、B、C 属于图 G2。连接这两者的灰色线表示在此当前状态下，节点 1 映射到节点 A，节点 2 映射到节点 B，等等。黄色边只是已覆盖（映射）节点的邻居。此处，$T_1$ 包含红色节点（4、5、6），它们是已覆盖节点 1、2、3 的邻居，而 $T_2$ 包含灰色节点（D、E、F）。图中所示的任何节点都不会包含在 $\tilde{T_1}$ 或 $\tilde{T_2}$ 中。后者集合将包含来自这两个图的所有剩余节点。

关于这些集合的计算，使用蛮力方法并在算法的每个步骤中迭代所有节点以查找所需节点并计算 $T_i$ 和 $\tilde{T_i}$ 在实践中并不实用。我们使用以下观察结果来实现 $T_i$ 和 $\tilde{T_i}$ 的增量计算，并使 VF2++ 更有效率。

  • 由于没有映射节点（$m=\varnothing$），因此没有映射节点的邻居，所以 $T_i$ 最初为空。
  • $\tilde{T_i}$ 最初包含来自图 $G_i, i=1,2$ 的所有节点，如果我们认为 $m$ 和 $T_1$ 都是空集，则可以直接从符号中实现这一点。
  • 算法的每个步骤都会将一个节点 $u$ 添加到映射中或从中弹出。

我们可以得出结论，在每个步骤中，$T_i$ 和 $\tilde{T_i}$ 可以增量更新。这种方法避免了大量冗余操作，并带来显着的性能改进。

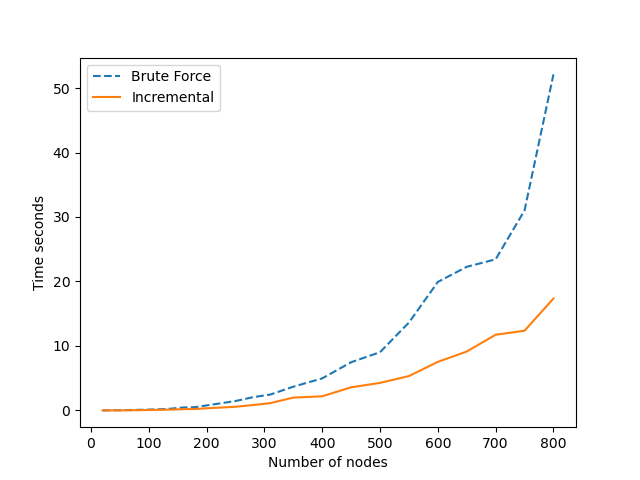
Performance comparison between brute force Ti computing and incremental updating.

上图显示了使用穷举蛮力法和增量更新 $T_i$ 和 $\tilde{T_i}$ 之间的性能差异。用于获得这些测量的图是一个具有边概率等于 $0.7$ 的规则GNP 图。可以清楚地看到，随着节点/边的数量增加，蛮力方法的执行时间比增量更新方法增加得快得多，正如预期的那样。蛮力方法如下所示

def compute_Ti(G1, G2, mapping, reverse_mapping):
    T1 = {nbr for node in mapping for nbr in G1[node] if nbr not in mapping}
    T2 = {
        nbr
        for node in reverse_mapping
        for nbr in G2[node]
        if nbr not in reverse_mapping
    }

    T1_out = {n1 for n1 in G1.nodes() if n1 not in mapping and n1 not in T1}
    T2_out = {n2 for n2 in G2.nodes() if n2 not in reverse_mapping and n2 not in T2}
    return T1, T2, T1_out, T2_out

如果我们假设 G1 和 G2 具有相同数量的节点 (N)，映射中的节点平均数为 $N_m$，并且图的平均节点度为 $D$，则此函数的时间复杂度为

$$O(2N_mD + 2N) = O(N_mD + N)$$

其中我们排除了 $T_i$、$mapping$ 和 $reverse\_mapping$ 中的查找时间，因为它们都是 $O(1)$。我们的增量方法如下所示

def update_Tinout(
    G1, G2, T1, T2, T1_out, T2_out, new_node1, new_node2, mapping, reverse_mapping
):
    # This function should be called right after the feasibility is established and node1 is mapped to node2.
    uncovered_neighbors_G1 = {nbr for nbr in G1[new_node1] if nbr not in mapping}
    uncovered_neighbors_G2 = {
        nbr for nbr in G2[new_node2] if nbr not in reverse_mapping
    }

    # Add the uncovered neighbors of node1 and node2 in T1 and T2 respectively
    T1.discard(new_node1)
    T2.discard(new_node2)
    T1 = T1.union(uncovered_neighbors_G1)
    T2 = T2.union(uncovered_neighbors_G2)

    # todo: maybe check this twice just to make sure
    T1_out.discard(new_node1)
    T2_out.discard(new_node2)
    T1_out = T1_out - uncovered_neighbors_G1
    T2_out = T2_out - uncovered_neighbors_G2

    return T1, T2, T1_out, T2_out

根据之前的符号，它是

$$O(2D + 2(D + M_{T_1}) + 2D) = O(D + M_{T_1})$$

其中 $M_{T_1}$ 是 $T_1$ 中元素的预期（平均）数量。

当然，在这种情况下，复杂度要好得多，因为 $D$ 和 $M_{T_1}$ 明显小于 $N_mD$ 和 $N$。

在这篇文章中，我们从高层次上研究了节点排序是如何工作的，以及我们如何能够计算一些重要的参数来减少空间和时间复杂度。下一篇文章将继续考察 VF2++ 算法的另外两个重要组成部分：候选节点对选择和决定何时应该或不应该扩展映射的剪枝/一致性规则。敬请期待！