
我现在已经完成了对 1970 年 Micheal Held 和 Richard M. Karp 的论文《旅行商问题与最小生成树》中详述的上升法和分支定界法的实现。在我的上一篇名为 理解上升法 的文章中,我完成了上升法的第一次迭代,并发现了 find_epsilon() 方法中的一个重要错误,并找到了更有效的方法来确定图中的替代节点。但是,给出的解决方案仍然不是最优解。
在与我的 GSoC 导师讨论了我的选择后,我决定继续进行分支定界法,希望由于该方法更易于人工计算,并且 Held 和 Karp 在论文中给出了一个示例,因此我将能够找到剩余的缺陷。幸运的是,情况确实如此,我能够正确地实现分支定界法并修复上升法中的最后一个问题。
分支定界法的初始实现#
分支定界法源于上升法,但调整了我们确定上升方向的方式,并简化了 $\epsilon$ 的表达式。作为提醒,我们使用失衡顶点的概念来查找上升方向,这些方向是单位向量或负单位向量。失衡顶点是指在图的最小 1-树集上,始终连接不足或连接过多的顶点。正式定义在第 1151 页给出,如下所示:
如果对于所有 $k \in K(\pi)$,都有 $v_{ik} \geqq 1$,则称顶点 $i$ 在点 $\pi$ 处为失衡高;类似地,如果对于所有 $k \in K(\pi)$,都有 $v_{ik} = -1$,则称顶点 $i$ 在点 $\pi$ 处为失衡低。
其中 $v_{ik}$ 是顶点的度数减去 2。首先,我创建了一个名为 direction_of_ascent_kilter() 的函数,该函数根据顶点是否失衡返回上升方向。但是,我没有使用 Held 和 Karp 在论文中提到的方法,即查找 $K(\pi, u_i)$ 中的一个成员,其中 $u_i$ 是第 $i$ 个位置为 1 的单位向量,并检查顶点 $i$ 的度数是否为 1 或大于 2。相反,我知道我可以使用现有的代码找到 $K(\pi)$ 的元素,并决定检查所有 $k \in K(\pi)$ 的 $v_{ik}$ 值,并且一旦确定某个顶点失衡,就简单地转到下一个顶点。
一旦我获得了所有顶点到其失衡状态的映射,就找到一个失衡的顶点并返回相应的上升方向。
对 find_epsilon() 的更改非常小,基本上是从 $\epsilon$ 的公式中删除了分母,并添加了一个检查,以查看我们是否具有负的上升方向,以便交叉距离变为正数,从而有效。
需要的新函数是 branch(),它根据 Held 和 Karp 论文进行分支。它首先运行线性程序以形成上升法以确定是否存在上升方向。如果方向确实存在,则分支。否则,在最小 1-树集中搜索一个回路,然后如果不存在,则分支。分支过程本身相当简单,找到第一条开放边(不在分区集 $X$ 和 $Y$ 中的边),然后创建两个新的配置,其中该边分别包含或排除。
最后,算法的整体结构,用伪代码编写如下:
Initialize pi to be the zero vector.
Add the configuration (∅, ∅, pi, w(0)) to the configuration priority queue.
while configuration_queue is not empty:
config = configuration_queue.get()
dir_ascent = direction_of_ascent_kilter()
if dir_ascent is None:
branch()
if solution returned by branch is not None
return solution
else:
max_dist = find_epsilon()
update pi
update edge weights
update config pi and bound value
调试分支定界法#
我最初实现的分支定界法返回了与上升法相同的错误解决方案,但边权重不同。作为提醒,我想要一个看起来像这样的解决方案:

我现在有两个算法返回此解决方案:

正如我之前提到的,分支定界法比上升法更容易人工计算,因此我决定将我的实现的执行与 [1] 中给出的执行进行比较。下面,左侧是 Held 和 Karp 论文中的数据,右侧是我的程序在有向版本上的执行情况。
| 无向图 | 有向图 |
|---|---|
| 迭代 1 | |
| 起始配置:$(\emptyset, \emptyset, \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}, 196)$ | 起始配置:$(\emptyset, \emptyset, \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}, 196)$ |
| 最小 1-树 | 最小 1-树 |
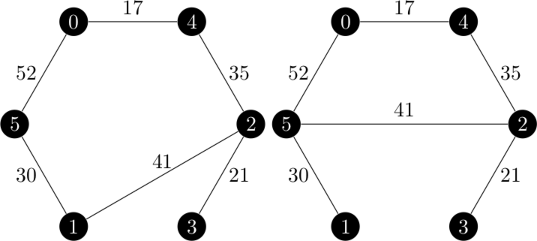 |
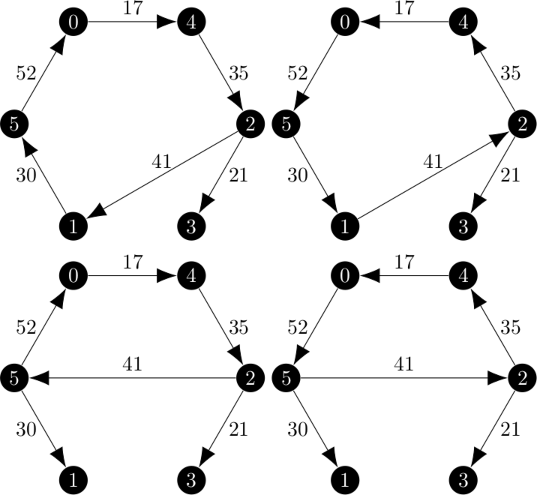 |
| 顶点 3 失衡低 | 顶点 3 失衡低 |
| $d = \begin{bmatrix} 0 & 0 & 0 & -1 & 0 & 0 \end{bmatrix}$ | $d = \begin{bmatrix} 0 & 0 & 0 & -1 & 0 & 0 \end{bmatrix}$ |
| $\epsilon(\pi, d) = 5$ | $\epsilon(\pi, d) = 5$ |
| 新配置:$(\emptyset, \emptyset, \begin{bmatrix} 0 & 0 & 0 & -5 & 0 & 0 \end{bmatrix}, 201)$ | 新配置:$(\emptyset, \emptyset, \begin{bmatrix} 0 & 0 & 0 & -5 & 0 & 0 \end{bmatrix}, 212)$ |
| 迭代 2 | |
| 最小 1-树 | 最小 1-树 |
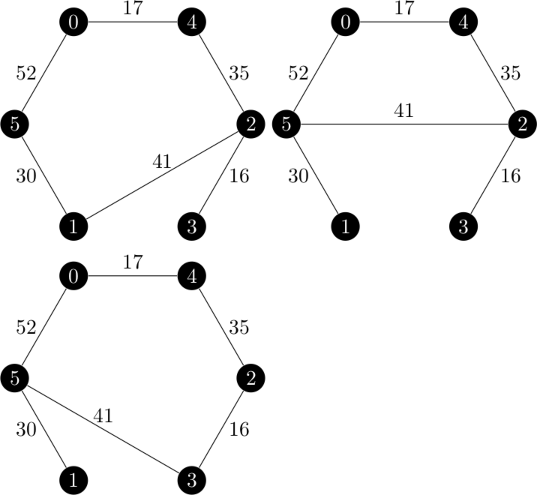 |
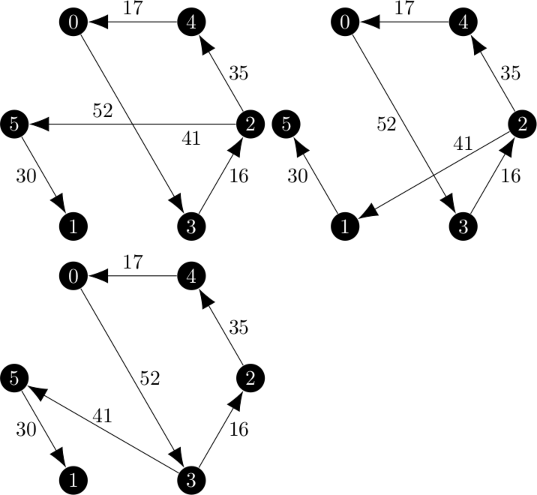 |
为了获得这些结果,我禁止程序能够选择将顶点 0 连接到同一其他顶点作为入边和出边。但是,很明显,从一开始,迭代二就不可能相同。
我注意到在第一次迭代中,1-树的个数是 1-树的两倍,区别在于循环可以双向遍历。这在 1-树和 1-树之间建立了映射。在第二次迭代中,1-树的个数不是 1-树的两倍,并且该映射不存在。顶点 0 始终在树中连接到顶点 3 和顶点 5。此外,1-树的成本高于 1-树的成本。
我知道树中根节点的选择会影响上升法中的总价格。我现在想知道最小 1-树是否可以来自非最小生成树。答案是肯定的。
为了检验这个假设,我使用 k_pi() 的修改版本创建了一个简单的 Python 脚本。整个脚本比我想在这里展示的要长,但要点很简单;遍历图中的所有生成树,跟踪最小权重,然后打印该程序找到的最小 1-树,以与未修改的程序找到的进行比较。
输出如下:
Adding arborescence with weight 212.0
Adding arborescence with weight 212.0
Adding arborescence with weight 212.0
Adding arborescence with weight 204.0
Adding arborescence with weight 204.0
Adding arborescence with weight 196.0
Adding arborescence with weight 196.0
Adding arborescence with weight 196.0
Adding arborescence with weight 196.0
Adding arborescence with weight 196.0
Adding arborescence with weight 196.0
Found 6 minimum 1-arborescences
(1, 5, 30)
(2, 1, 41)
(2, 3, 21)
(4, 2, 35)
(5, 0, 52)
(0, 4, 17)
(1, 2, 41)
(2, 3, 21)
(2, 4, 35)
(4, 0, 17)
(5, 1, 30)
(0, 5, 52)
(2, 3, 21)
(2, 4, 35)
(4, 0, 17)
(5, 1, 30)
(5, 2, 41)
(0, 5, 52)
(2, 4, 35)
(3, 2, 16)
(4, 0, 17)
(5, 1, 30)
(5, 3, 46)
(0, 5, 52)
(2, 3, 21)
(3, 5, 41)
(4, 2, 35)
(5, 1, 30)
(5, 0, 52)
(0, 4, 17)
(2, 3, 21)
(2, 5, 41)
(4, 2, 35)
(5, 1, 30)
(5, 0, 52)
(0, 4, 17)
这很有启发意义。权重为 212 的 1-树是我在第二次迭代中使用的分支定界法使用的,但不是真正的最小 1-树。从图形上看,这六个 1-树看起来像这样:

突然,1-树和 1-树之间的映射又回来了!但是为什么最小 1-树可以来自非最小生成树?请记住,我们通过在顶点集 ${2, 3, \dots, n}$ 上查找生成树,然后将缺失的顶点连接到生成树的根和最小权重的入边来创建 1-树。
这意味着即使在真正的最小生成树中,1-树的最终权重也会根据将“顶点 1”连接到树根的成本而变化。在上升法的实现过程中,我之前已经不得不处理这个问题。现在假设图中的每个顶点都不是生成树集中树的根。令最小根为连接成本最低的树的根顶点,令最大根为连接成本最高的树的根顶点。如果需要,我们可以根据从“顶点 1”到该根的边的权重将根从最小到最大排序。
最后,假设仅考虑最小生成树集的结果是得到一组最小 1-树,这些树不使用最小根,并且总成本比最小生成树的成本加上连接到最小根的成本多 $c$。继续考虑权重递增的生成树,例如 ArborescenceIterator 返回的那些。最终,ArborescenceIterator 将返回一个具有最小根的生成树。如果最小生成树的成本为 $c_{min}$,并且此树的成本小于 $c_{min} + c$,则从非最小生成树中找到了一个新的最小 1-树。
显然,考虑图中的所有生成树是不切实际的,并且由于 ArborescenceIterator 按权重递增的顺序返回树,因此存在一个权重,在此权重之后不可能产生最小 1-树。
假设最小生成树形图的成本为 $c_{min}$,连接根节点的总成本范围从 $r_{min}$ 到 $r_{max}$。最小 1-树形图的最坏情况成本为 $c_{min} + r_{max}$,这将最小生成树形图连接到最昂贵的根节点;而最佳情况最小 1-树形图的成本为 $c_{min} + r_{min}$。关于生成树形图本身的权重,一旦它超过 $c_{min} + r_{max} - r_{min}$,我们就知道了即使它使用最小根节点,总权重也将大于最坏情况下的最小 1-树形图,因此这是我们使用 ArborescenceIterator 的边界。
在实现此边界以检查生成树形图以查找最小 1-树形图后,两种方法都在测试图上成功执行。
后续步骤#
现在,上升法和分支定界法都已运行,必须对其进行准确性和性能测试。令人惊讶的是,在我一直在使用的测试图(最初来自 Held 和 Karp 的论文)上,上升法比分支定界法快 2 到 3 倍。但是,这个六顶点图很小,分支定界法在更大的图上可能仍然具有更好的性能。我将需要创建更大的测试图,然后选择总体性能更好的方法。
此外,这是一个 $f(\pi)$(环路与 1-树形图之间的差距)收敛到 0 的示例。情况并非总是如此,因此我需要在一个最小差距大于 0 的示例上进行测试。
最后,我的 Held Karp 松弛程序的输出是一个环路。这仅仅是 Asadpour 非对称旅行商问题的其中一部分,该算法采用基于松弛最终结果生成的修改后的向量。我仍然需要转换输出以匹配我今年夏天计划实现的整体算法的预期。
我希望在 6 月 30 日或 7 月 1 日开始 Asadpour 算法的下一步。
参考文献#
[1] Held, M., Karp, R.M. 旅行商问题与最小生成树. 运筹学,1970-11-01,第 18 卷(6),第 1138-1162 页。 https://www.jstor.org/stable/169411