Final mosaic

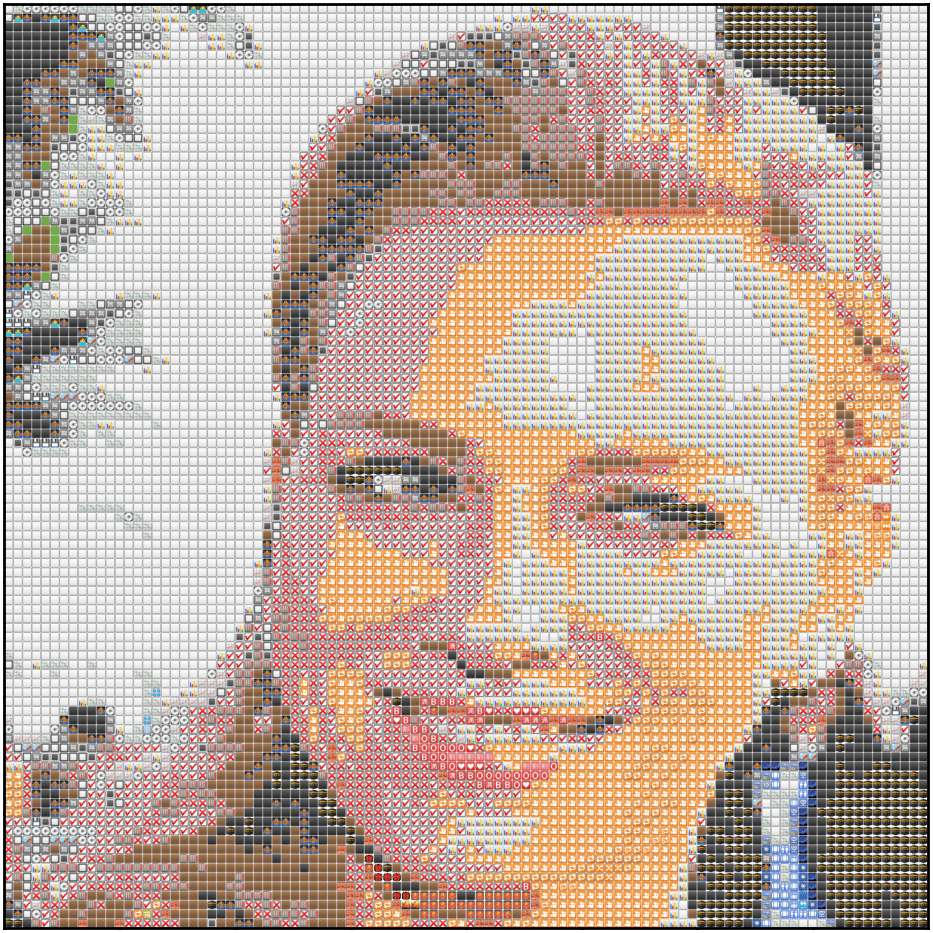
有一段时间，我偶然发现了一个很酷的 代码库，它可以从图像中创建表情符号艺术。我想用它将我枯燥的 Facebook 个人资料图片转换为更时髦的东西。唯一的麻烦是？它用 Rust 编写。

所以，我没有安装 Rust，而是选择了简单的方法，使用 matplotlib 在 Python 中编写一些代码来实现相同的功能。

因为这是任何理智的人都会做的事，对吧？

在这篇文章中，我会尝试解释我的过程，我们尝试重新创建类似于下面的马赛克。我把这篇文章的目标读者定为之前使用过某种图像数据的人；但实际上，任何人都可以跟着做。

Emoji mosaic by Will Dady based on Andy Warhol’s Multiple Marilyns.

包#

import numpy as np
from tqdm import tqdm
from scipy import spatial
from matplotlib import cm
import matplotlib.pyplot as plt
import matplotlib
import scipy


print(f"Matplotlib:{matplotlib.__version__}")
print(f"Numpy:{np.__version__}")
print(f"Scipy: {scipy.__version__}")

## Matplotlib: '3.2.1'
## Numpy: '1.18.1'
## Scipy: '1.4.1'

让我们读取我们的图像

img = plt.imread(r"naomi_32.png", 1)
dim = img.shape[0] ##we'll need this later
plt.imshow(img)

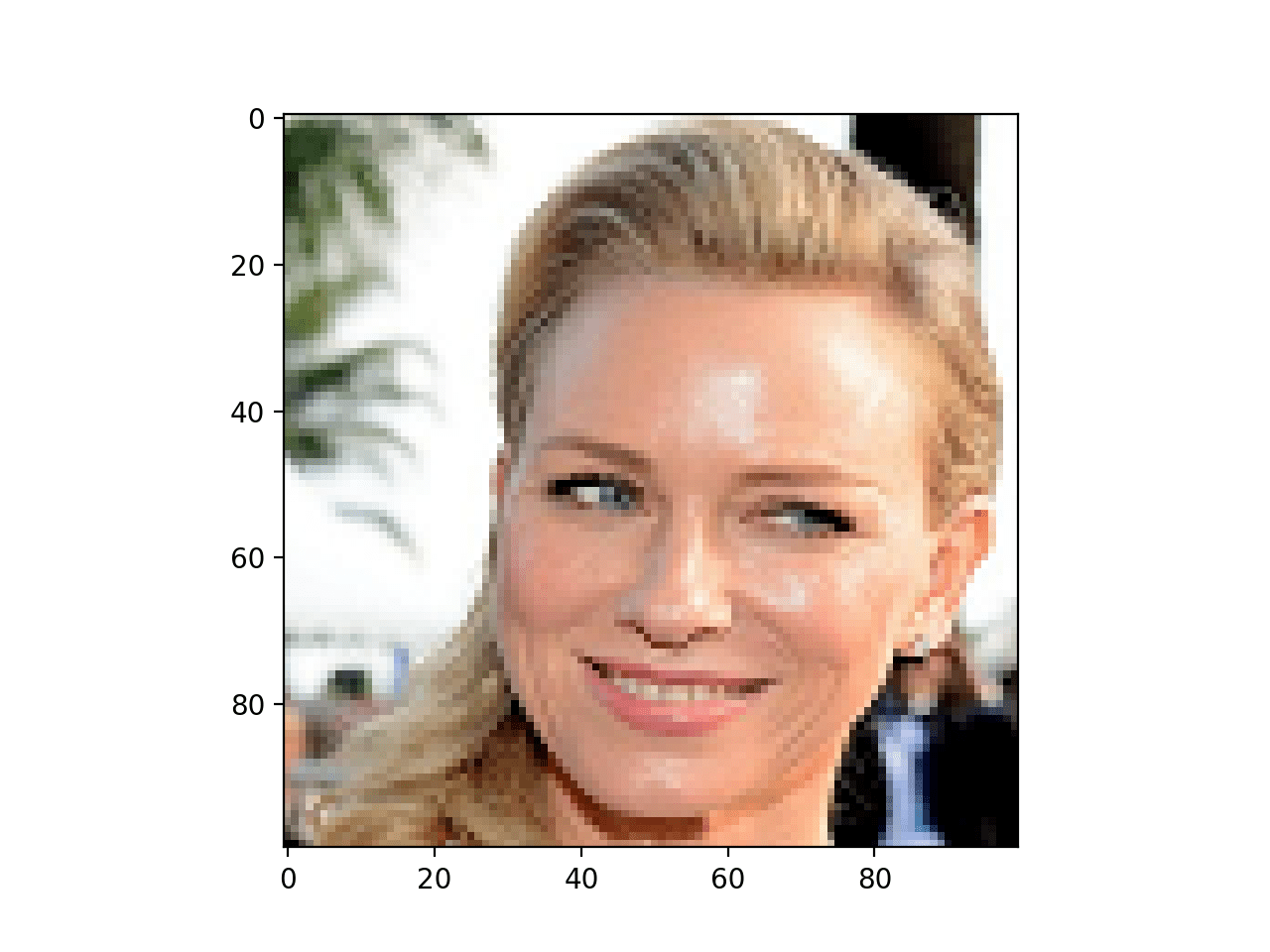
Naomi Watts Cannes (2014) Licensed under Creative Commons attributed to Georges Biard

注意：上面显示的图像大小为 100x100，但从这里开始我们将使用 32x32，因为这足以满足我们的所有需求。

所以实际上，图像到底是什么？对于 numpy 和 matplotlib（以及几乎所有其他图像处理库来说），它本质上只是一个矩阵（例如 A），其中每个像素（p）都是 A 的一个元素。如果它是一个灰度图像，那么每个像素（p）只是一个单一数字（或标量）——如果为浮点数，则在 [0,1] 范围内，如果为整数，则在 [0,255] 范围内。如果它不是灰度图像——就像我们的情况一样——那么每个像素都是一个三维向量（RGB）——**红色** (R)、**绿色** (G) 和 **蓝色** (B)，或者一个四维向量 RGBA (A 代表 **Alpha**，它基本上是透明度)。

如果到目前为止有任何不清楚的地方，我强烈建议您阅读类似于 这篇文章 或 这篇文章。了解图像可以表示为矩阵（或 numpy 数组）非常有用，因为几乎所有的图像变换都可以用矩阵数学表示。

为了证明我的观点，让我们看一下 img。

## Let's check the type of img
print(type(img))
# <class 'numpy.ndarray'>

## The shape of the array img
print(img.shape)
# (32, 32, 4)

## The value of the first pixel of img
print(img[0][0])
# [128 144 117 255]

## Let's view the color of the first pixel
fig, ax = plt.subplots()
color = img[0][0] / 255.0  ##RGBA only accepts values in the 0-1 range
ax.fill([0, 1, 1, 0], [0, 0, 1, 1], color=color)

这应该会给你一个填充了 img 的第一个像素颜色的正方形。

img[0][0]

方法#

我们想要从普通图像转变为充满表情符号的图像——或者换句话说，**图像的图像**。本质上，我们将用表情符号替换所有像素。但是，为了确保我们新的表情符号图像看起来像原始图像，而不是随机的笑脸，诀窍是确保每个像素都被替换为一个颜色与该像素相似的表情符号。这就是赋予结果马赛克外观的原因。

“相似”实际上只是意味着表情符号的**平均**（中位数也值得尝试）颜色应该接近它所替换的像素。

那么如何找到整个图像的平均颜色呢？很简单。我们只需要将所有 RGBA 数组取平均值，将 R 值加在一起，然后将 G 值加在一起，然后将 B 值加在一起，然后将 A 值加在一起（顺便说一下，A 值在我们这里都是 1，所以平均值也将是 1）。下面是正式表达的这个想法

\[ (r, g, b){\mu}=\left(\frac{\left(r{1}+r_{2}+\ldots+r_{N}\right)}{N}, \frac{\left(g_{1}+g_{2}+\ldots+g_{N}\right)}{N}, \frac{\left(b_{1}+b_{2}+\ldots+b_{N}\right)}{N}\right) \]

最终的颜色将是一个包含 RGBA 值的单个数组：\[ [r_{\mu}, g_{\mu}, b_{\mu}, 1] \]

所以现在我们的步骤变得有点像这样

第一部分 - 获取表情符号匹配

  1. 找到一堆表情符号。
  2. 找到表情符号的平均值。
  3. 对于图像中的每个像素，找到与之最接近的表情符号（颜色方面），并用该表情符号（例如 E）替换像素。

第二部分 - 将表情符号重新塑造成图像

  1. 将所有 E 的扁平化数组重新塑造成我们图像的形状。
  2. 将所有表情符号连接成一个数组（减少维度）。

就是这样！

步骤 I.1 - 我们的表情符号库#

我之前用一些 BeautifulSoup 和 requests 魔法为你处理好了。我们的表情符号集合是一个形状为 1506, 16, 16, 4 的 numpy 数组——即 1506 个表情符号，每个表情符号都是一个 16x16 的 RGBA 值数组。你可以在 这里 找到它。

emoji_array = np.load("emojis_16.npy")
print(emoji_array.shape)
## 1506, 16, 16, 4

##plt.imshow(emoji_array[0]) ##to view the first emoji

步骤 I.2 - 计算所有表情符号的平均 RGBA 值。#

我们已经看到了上面的公式；这是用 numpy 代码实现的。我们将迭代所有 1506 个表情符号，并从它们中创建一个数组 emoji_mean_array。

emoji_mean_array = np.array(
    [ar.mean(axis=(0, 1)) for ar in emoji_array]
)  ##`np.median(ar, axis=(0,1))` for median instead of mean

步骤 I.3 - 查找所有像素最接近的表情符号匹配#

最简单的方法是使用 Scipy 的 KDTree 创建一个所有平均 RGBA 值的 tree 对象，我们在 #2 中计算过。这使我们能够使用 query 方法对每个像素进行快速查找。以下是代码示例 -

tree = spatial.KDTree(emoji_mean_array)

indices = []
flattened_img = img.reshape(-1, img.shape[-1])  ##shape = [1024, 16, 16, 4]
for pixel in tqdm(flattened_img, desc="Matching emojis"):
    _, index = tree.query(pixel)  ##returns distance and index of closest match.
    indices.append(index)

emoji_matches = emoji_array[indices]  ##our emoji_matches

步骤 II.1#

最后一步是稍微重新调整数组的形状，以便我们能够使用 imshow 函数来绘制它。如上所示，为了遍历像素，我们不得不将图像扁平化成 flattened_img。现在我们必须将其恢复到图像的形式。幸运的是，使用 numpy 的 reshape 函数可以轻松实现这一点。

resized_ar = emoji_matches.reshape(
    (dim, dim, 16, 16, 4)
)  ##dim is what we got earlier when we read in the image

步骤 II.2#

最后一点是最棘手的。我们目前得到的输出的问题是，它嵌套得太多了。或者用更简单的术语来说，我们现在得到的是一张图像，其中每个像素本身都是一张图像。这很好，但它不是 imshow 的有效输入，如果我们尝试将其传递进去，它会告诉我们这一点。

TypeError: Invalid shape (32, 32, 16, 16, 4) for image data

为了直观地理解我们的问题，可以这样想。我们现在拥有的是很多这样的图像

“Chopped raccoon img”

我们想要将它们全部合并在一起。就像这样

“Rejoined raccoon img”

从稍微更技术性的角度来看，我们现在拥有的是一个五维数组。我们需要将其重新塑造成最多三维的数组。但是，这并不像简单地使用 np.reshape 那么容易（我建议您还是先尝试一下）。

不过不用担心，我们有 Stack Overflow 来救场！这个优秀的 答案 就是这么做的。您不需要查看它，我已经将相关代码复制到这里。

def np_block_2D(chops):
    """Converts list of chopped images to one single image"""
    return np.block([[[x] for x in row] for row in chops])


final_img = np_block_2D(resized_ar)

print(final_img.shape)
## (512, 512, 4)

形状看起来足够正确。让我们尝试绘制它。

plt.imshow(final_img)

“Emoji Mosaic final_img”

瞧！

当然，结果看起来有点不好，但那是因为我们只使用了 32x32 的表情符号。以下是使用 10000 个表情符号（100x100）时，相同代码的输出。

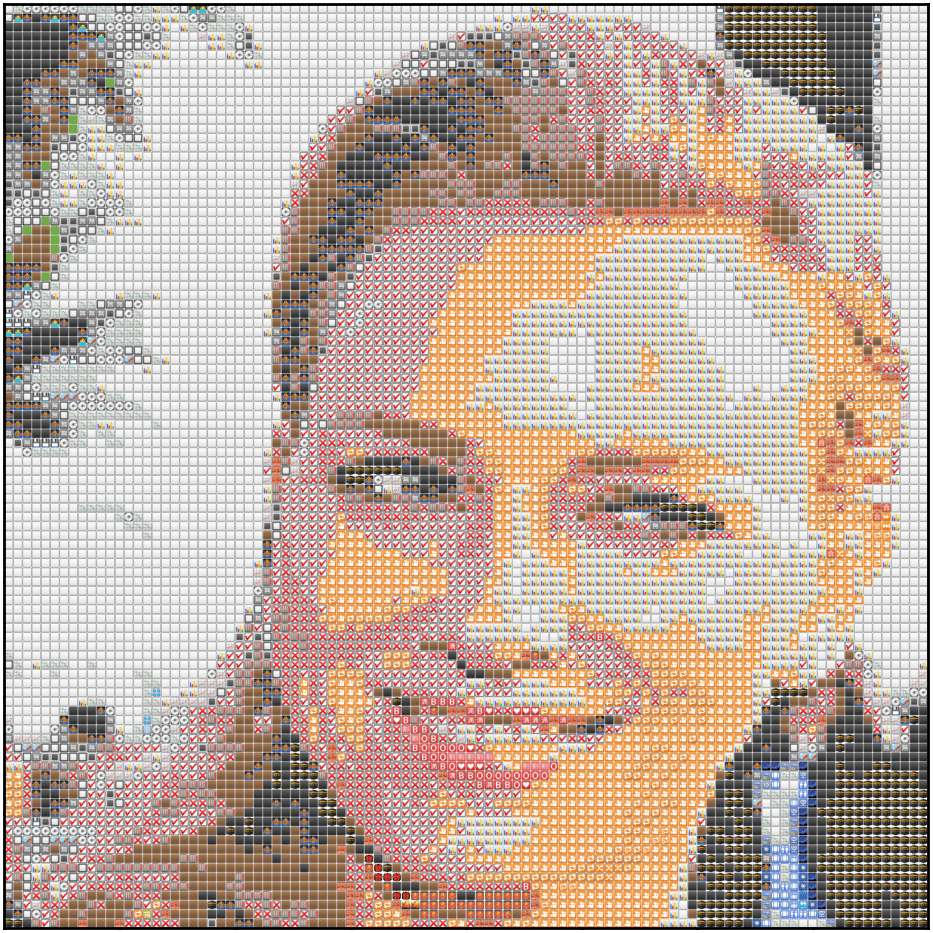
“Emoji Mosaic full_size”

好些了吗？

现在，让我们尝试创建九个这样的表情符号图像，并将它们一起网格化。

def canvas(gray_scale_img):
    """
    Plot a 3x3 matrix of the images using different colormaps
        param gray_scale_img: a square gray_scale_image
    """
    fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(13, 8))
    axes = axes.flatten()

    cmaps = [
        "BuPu_r",
        "bone",
        "CMRmap",
        "magma",
        "afmhot",
        "ocean",
        "inferno",
        "PuRd_r",
        "gist_gray",
    ]
    for cmap, ax in zip(cmaps, axes):
        cmapper = cm.get_cmap(cmap)
        rgba_image = cmapper(gray_scale_img)
        single_plot(rgba_image, ax)
        # ax.imshow(rgba_image) ##try this if you just want to plot the plain image in different color spaces, comment the single_plot call above
        ax.set_axis_off()

    plt.subplots_adjust(hspace=0.0, wspace=-0.2)
    return fig, axes

这段代码与之前的代码基本相同。为了获得不同的颜色，我使用了一个简单的技巧。我首先将图像转换为灰度，然后对其应用 9 种不同的颜色映射。然后，我使用颜色映射返回的 RGB 值来获取我们新输入图像的绝对值。之后，剩下的唯一部分就是将新的输入图像通过我们已经讨论过的管道，这样就得到了我们的表情符号图像。

下面是示例

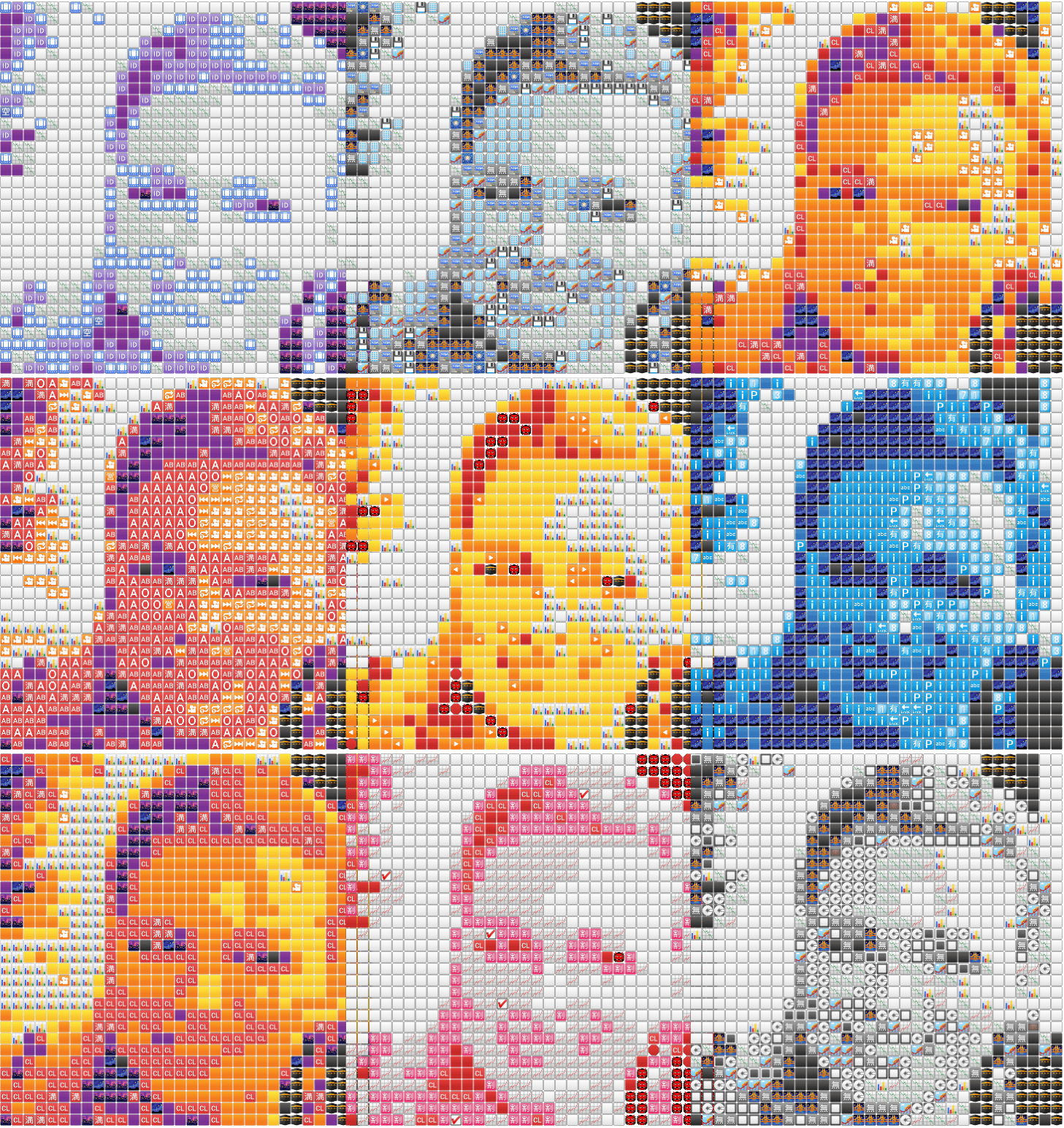
“Emoji Mosaic 3x3_grid”

漂亮

结论#

一些最终的想法，作为总结。

  • 我不确定我使用不同的颜色映射来获取不同颜色的方法是否与人们通常的做法一致。我几乎可以肯定有更好的方法，如果您知道的话，请向代码库（链接在下面）提交一个 PR。

  • 遍历每个像素并不是最好的方法。我们侥幸成功了，因为只有 1024（32x32）个像素，但对于分辨率更高的图像，我们必须要么一次遍历图像网格（例如 3x3 或 2x2 窗口），要么调整图像本身的大小，使其更易于处理。我更喜欢后者，因为这样我们也可以在同一个调用中将其调整为正方形形状，这也有额外的优势，可以很好地融入我们的 3x3 马赛克中。我会让读者自行使用 numpy 来解决这个问题（并且，不，请不要使用 cv2.resize）。

  • KDTree 不是我初始代码的一部分。最初，我会遍历每个表情符号，然后计算每个像素，然后计算欧几里得距离（使用 np.linalg.norm(a-b)）。正如您可能想象的那样，那里的嵌套循环大大降低了代码的速度——即使是 32x32 的表情符号图像也需要大约 10 分钟才能运行——现在相同的代码大约需要 19 秒。我想这就是向量化的力量！

  • 值得用中位数代替平均值来获取表情符号的 RGBA 值。大多数表情符号都是圆形的，因此圆形区域之外有很多空白区域，这会淡化平均颜色，进而淡化最终结果。考虑中位数可能会解决某些图像（不是非常丰富的图像）的这个问题。

  • 虽然我尝试以线性方式（我希望）以良好的解释和代码组合的方式进行，但我强烈建议您查看代码库中 这里 的完整代码，以防您感觉我突然抛出了一些东西。

我希望您喜欢这篇文章，并从中有所收获。如果您有任何反馈、批评、问题，请随时通过 Twitter 发送私信给我，或给我发邮件（最好是前者，因为我几乎一直都在那里）。谢谢，保重！