A colourful outline of a bunny.

Matplotlib 有一个非常棒的3D 接口，它拥有许多功能（也有一些限制），并且在用户中非常受欢迎。然而，对于一些用户（或者可能是大多数用户）来说，3D 渲染仍然被认为是一种“魔法”。因此，我想在这篇文章中解释一下，一旦你理解了一些基本概念，3D 渲染其实非常简单。为了证明这一点，我们将使用 60 行 Python 代码和一个 Matplotlib 调用来渲染上面的兔子模型。也就是说，我们不会使用 3D 轴。

广告：这篇文章来自一本即将出版的关于使用 Python 和 Matplotlib 进行科学可视化的开放获取书籍。如果您想支持我的工作并提前访问这本书，请访问https://github.com/rougier/scientific-visualization-book。

加载兔子模型#

首先，我们需要加载我们的模型。我们将使用斯坦福兔子模型的简化版本。该文件使用Wavefront 格式，这是一种最简单的格式之一，因此让我们编写一个非常简单的（但容易出错的）加载器，它只需完成这篇文章（以及这个模型）所需的任务。

V, F = [], []
with open("bunny.obj") as f:
   for line in f.readlines():
       if line.startswith('#'):
           continue
       values = line.split()
       if not values:
           continue
       if values[0] == 'v':
           V.append([float(x) for x in values[1:4]])
       elif values[0] == 'f':
           F.append([int(x) for x in values[1:4]])
V, F = np.array(V), np.array(F)-1

V 现在是一组顶点（如果你愿意，可以称为 3D 点），F 是一组面（= 三角形）。每个三角形由 3 个相对于顶点数组的索引描述。现在，让我们标准化顶点，以便整个兔子模型适应单位盒。

V = (V-(V.max(0)+V.min(0))/2)/max(V.max(0)-V.min(0))

现在，我们可以通过仅获取顶点的 x、y 坐标并去除 z 坐标来初步查看模型。为此，我们可以使用功能强大的PolyCollection 对象，它允许高效地渲染非规则多边形集合。由于我们想要渲染一堆三角形，因此这是一个完美的匹配。所以让我们首先提取三角形并去除z 坐标。

T = V[F][...,:2]

现在我们可以渲染它了。

fig = plt.figure(figsize=(6,6))
ax = fig.add_axes([0,0,1,1], xlim=[-1,+1], ylim=[-1,+1],
                  aspect=1, frameon=False)
collection = PolyCollection(T, closed=True, linewidth=0.1,
                            facecolor="None", edgecolor="black")
ax.add_collection(collection)
plt.show()

你应该得到类似这样的结果（bunny-1.py）。

A black and white outline of a bunny facing left side.

透视投影#

我们刚刚进行的渲染实际上是正交投影，而上面的兔子使用了透视投影。

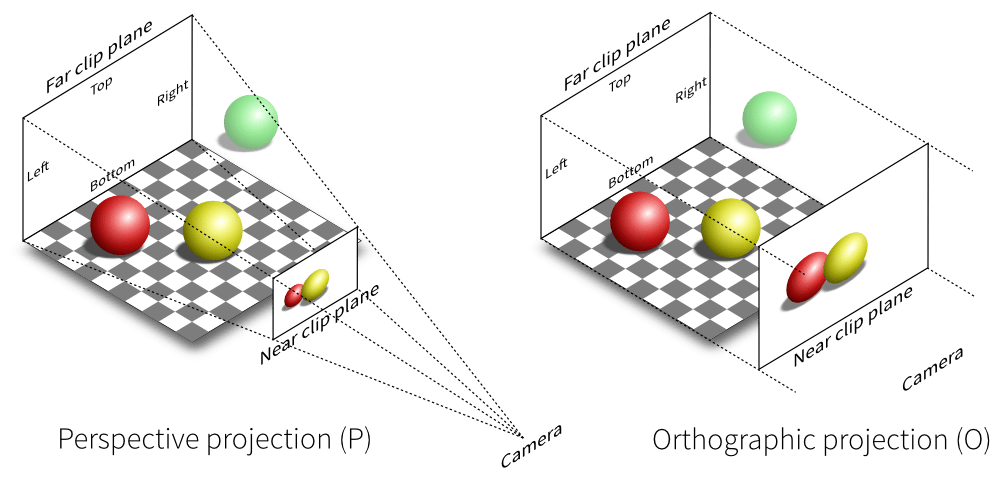
Difference in perspective projection and orthographic projection. The near clip plane appears smaller in the perspective projective than in the orthographic projection.

在这两种情况下，定义投影的正确方法是首先定义一个视景体，即我们要在屏幕上渲染的 3D 空间中的体积。为此，我们需要考虑 6 个裁剪平面（左、右、上、下、远、近），它们相对于相机包围视景体（平截头体）。如果我们定义一个相机位置和一个观察方向，则每个平面都可以用一个标量来描述。一旦我们有了这个视景体，我们就可以使用正交投影或透视投影将其投影到屏幕上。

对我们来说幸运的是，这些投影非常著名，并且可以用 4x4 矩阵表示。

def frustum(left, right, bottom, top, znear, zfar):
    M = np.zeros((4, 4), dtype=np.float32)
    M[0, 0] = +2.0 * znear / (right - left)
    M[1, 1] = +2.0 * znear / (top - bottom)
    M[2, 2] = -(zfar + znear) / (zfar - znear)
    M[0, 2] = (right + left) / (right - left)
    M[2, 1] = (top + bottom) / (top - bottom)
    M[2, 3] = -2.0 * znear * zfar / (zfar - znear)
    M[3, 2] = -1.0
    return M

def perspective(fovy, aspect, znear, zfar):
    h = np.tan(0.5*radians(fovy)) * znear
    w = h * aspect
    return frustum(-w, w, -h, h, znear, zfar)

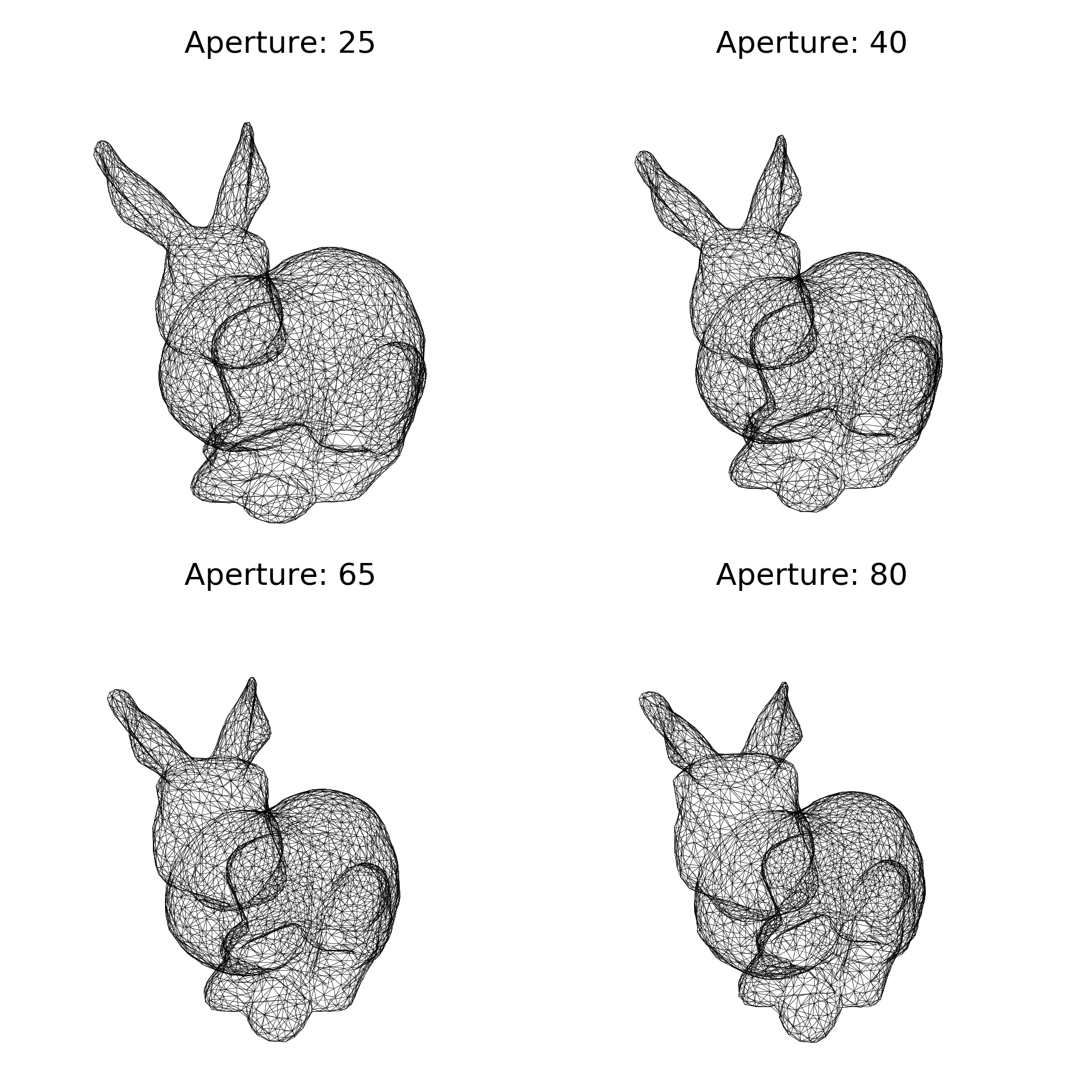
对于透视投影，我们还需要指定光圈角，它（或多或少）设置了近平面相对于远平面的尺寸。因此，对于高光圈，你会得到很多“变形”。

但是，如果你查看上面的两个函数，你会发现它们返回 4x4 矩阵，而我们的坐标是 3D 的。那么如何使用这些矩阵呢？答案是齐次坐标。长话短说，齐次坐标最适合处理 3D 中的变换和投影。在我们的例子中，因为我们处理的是顶点（而不是向量），所以我们只需要将 1 作为第四个坐标（w）添加到所有顶点中。然后我们可以使用点积应用透视变换。

V = np.c_[V, np.ones(len(V))] @ perspective(25,1,1,100).T

最后一步，我们需要重新标准化齐次坐标。这意味着我们将每个变换后的顶点除以最后一个分量（w），以便每个顶点的w始终为 1。

V /= V[:,3].reshape(-1,1)

现在我们可以再次显示结果了（bunny-2.py）。

哦，奇怪的结果。哪里出错了？问题在于相机实际上在兔子内部。为了进行正确的渲染，我们需要将兔子移开相机，或者将相机移开兔子。让我们执行后者。相机当前位于 (0,0,0) 处，并且沿着 z 方向向上看（因为存在平截头体变换）。因此，我们需要将相机在 z 负方向上稍微移开一点，并且**在透视变换之前**。

V = V - (0,0,3.5)
V = np.c_[V, np.ones(len(V))] @ perspective(25,1,1,100).T
V /= V[:,3].reshape(-1,1)

现在你应该得到（bunny-3.py）。

模型、视图、投影 (MVP)#

可能不太明显，但最后的渲染实际上是一个透视变换。为了使其更加明显，我们将围绕兔子旋转。为此，我们需要一些旋转矩阵 (4x4)，并且我们可以在此期间定义平移矩阵。

def translate(x, y, z):
    return np.array([[1, 0, 0, x],
                     [0, 1, 0, y],
                     [0, 0, 1, z],
                     [0, 0, 0, 1]], dtype=float)

def xrotate(theta):
    t = np.pi * theta / 180
    c, s = np.cos(t), np.sin(t)
    return np.array([[1, 0,  0, 0],
                     [0, c, -s, 0],
                     [0, s,  c, 0],
                     [0, 0,  0, 1]], dtype=float)

def yrotate(theta):
    t = np.pi * theta / 180
    c, s = np.cos(t), np.sin(t)
    return  np.array([[ c, 0, s, 0],
                      [ 0, 1, 0, 0],
                      [-s, 0, c, 0],
                      [ 0, 0, 0, 1]], dtype=float)

我们现在将要应用的变换分解为模型（局部变换）、视图（全局变换）和投影，以便我们可以计算一个全局 MVP 矩阵来一次完成所有操作。

model = xrotate(20) @ yrotate(45)
view  = translate(0,0,-3.5)
proj  = perspective(25, 1, 1, 100)
MVP   = proj  @ view  @ model

现在我们编写：

V = np.c_[V, np.ones(len(V))] @ MVP.T
V /= V[:,3].reshape(-1,1)

你应该得到（bunny-4.py）。

现在让我们稍微调整一下光圈，这样你就可以看到区别。请注意，我们还必须调整到相机的距离，以便兔子具有相同的表观尺寸（bunny-5.py）。

深度排序#

现在让我们尝试填充三角形（bunny-6.py）。

如你所见，结果“有趣”且完全错误。问题在于 PolyCollection 将按照给定的顺序绘制三角形，而我们希望它们从后到前绘制。这意味着我们需要根据它们的深度对它们进行排序。好消息是我们已经在应用 MVP 变换时计算了此信息。它存储在新的 z 坐标中。但是，这些 z 值是基于顶点的，而我们需要对三角形进行排序。因此，我们将采用平均 z 值作为三角形深度的代表。如果三角形相对较小且不交叉，则效果非常好。

T =  V[:,:,:2]
Z = -V[:,:,2].mean(axis=1)
I = np.argsort(Z)
T = T[I,:]

现在一切都正确渲染了（bunny-7.py）。

让我们使用深度缓冲区添加一些颜色。我们将根据每个三角形的深度对其进行着色。PolyCollection 对象的美妙之处在于，你可以使用 NumPy 数组指定每个三角形的颜色，所以让我们这样做。

zmin, zmax = Z.min(), Z.max()
Z = (Z-zmin)/(zmax-zmin)
C = plt.get_cmap("magma")(Z)
I = np.argsort(Z)
T, C = T[I,:], C[I,:]

现在一切都正确渲染了（bunny-8.py）。

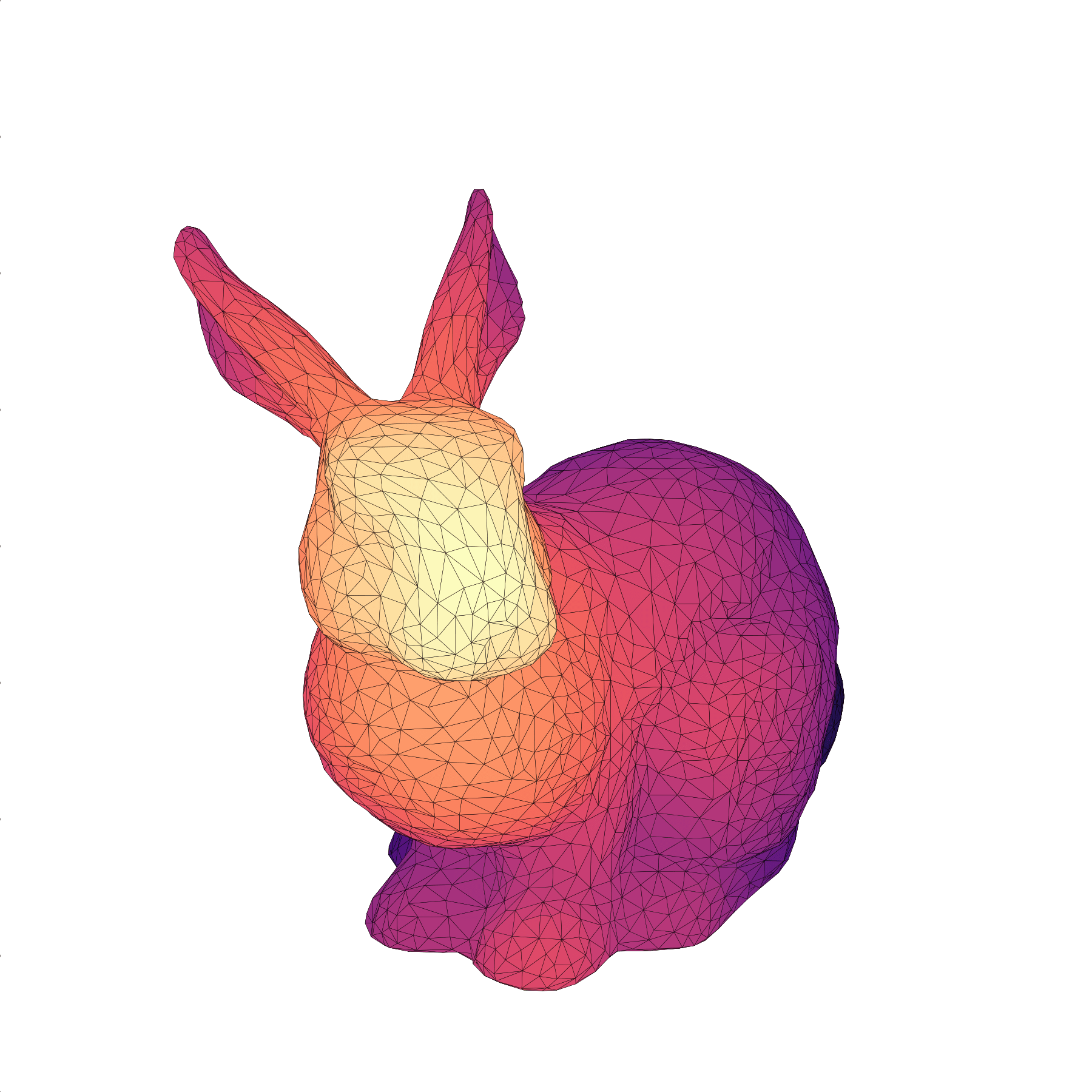
最终脚本只有 57 行（但几乎不可读）。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import PolyCollection

def frustum(left, right, bottom, top, znear, zfar):
    M = np.zeros((4, 4), dtype=np.float32)
    M[0, 0] = +2.0 * znear / (right - left)
    M[1, 1] = +2.0 * znear / (top - bottom)
    M[2, 2] = -(zfar + znear) / (zfar - znear)
    M[0, 2] = (right + left) / (right - left)
    M[2, 1] = (top + bottom) / (top - bottom)
    M[2, 3] = -2.0 * znear * zfar / (zfar - znear)
    M[3, 2] = -1.0
    return M
def perspective(fovy, aspect, znear, zfar):
    h = np.tan(0.5*np.radians(fovy)) * znear
    w = h * aspect
    return frustum(-w, w, -h, h, znear, zfar)
def translate(x, y, z):
    return np.array([[1, 0, 0, x], [0, 1, 0, y],
                     [0, 0, 1, z], [0, 0, 0, 1]], dtype=float)
def xrotate(theta):
    t = np.pi * theta / 180
    c, s = np.cos(t), np.sin(t)
    return np.array([[1, 0,  0, 0], [0, c, -s, 0],
                     [0, s,  c, 0], [0, 0,  0, 1]], dtype=float)
def yrotate(theta):
    t = np.pi * theta / 180
    c, s = np.cos(t), np.sin(t)
    return  np.array([[ c, 0, s, 0], [ 0, 1, 0, 0],
                      [-s, 0, c, 0], [ 0, 0, 0, 1]], dtype=float)
V, F = [], []
with open("bunny.obj") as f:
    for line in f.readlines():
        if line.startswith('#'):  continue
        values = line.split()
        if not values:            continue
        if values[0] == 'v':      V.append([float(x) for x in values[1:4]])
        elif values[0] == 'f' :   F.append([int(x) for x in values[1:4]])
V, F = np.array(V), np.array(F)-1
V = (V-(V.max(0)+V.min(0))/2) / max(V.max(0)-V.min(0))
MVP = perspective(25,1,1,100) @ translate(0,0,-3.5) @ xrotate(20) @ yrotate(45)
V = np.c_[V, np.ones(len(V))]  @ MVP.T
V /= V[:,3].reshape(-1,1)
V = V[F]
T =  V[:,:,:2]
Z = -V[:,:,2].mean(axis=1)
zmin, zmax = Z.min(), Z.max()
Z = (Z-zmin)/(zmax-zmin)
C = plt.get_cmap("magma")(Z)
I = np.argsort(Z)
T, C = T[I,:], C[I,:]
fig = plt.figure(figsize=(6,6))
ax = fig.add_axes([0,0,1,1], xlim=[-1,+1], ylim=[-1,+1], aspect=1, frameon=False)
collection = PolyCollection(T, closed=True, linewidth=0.1, facecolor=C, edgecolor="black")
ax.add_collection(collection)
plt.show()

现在轮到你来玩了。从这个简单的脚本开始，你可以获得有趣的结果。

使用 Matplotlib 创建自定义 3D 引擎

加载兔子模型#

透视投影#

模型、视图、投影 (MVP)#

深度排序#